Freidlin–Wentzell theorem
In mathematics, the Freidlin–Wentzell theorem is a result in the large deviations theory of stochastic processes. Roughly speaking, the Freidlin–Wentzell theorem gives an estimate for the probability that a (scaled-down) sample path of an Itō diffusion will stray far from the mean path. This statement is made precise using rate functions. The Freidlin–Wentzell theorem generalizes Schilder's theorem for standard Brownian motion.
Statement of the theorem
Let B be a standard Brownian motion on Rd starting at the origin, 0 ∈ Rd, and let Xε be an Rd-valued Itō diffusion solving an Itō stochastic differential equation of the form
where the drift vector field b : Rd → Rd is uniformly Lipschitz continuous. Then, on the Banach space C0 = C0([0, T]; Rd) equipped with the supremum norm ||·||∞, the family of processes (Xε)ε>0 satisfies the large deviations principle with good rate function I : C0 → R ∪ {+∞} given by
if ω lies in the Sobolev space H1([0, T]; Rd), and I(ω) = +∞ otherwise. In other words, for every open set G ⊆ C0 and every closed set F ⊆ C0,
and
References
- Freidlin, Mark I.; Wentzell, Alexander D. (1998). Random perturbations of dynamical systems. Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences] 260 (Second edition ed.). New York: Springer-Verlag. pp. pp. xii+430. ISBN 0-387-98362-7. MR1652127
- Dembo, Amir; Zeitouni, Ofer (1998). Large deviations techniques and applications. Applications of Mathematics (New York) 38 (Second edition ed.). New York: Springer-Verlag. pp. pp. xvi+396. ISBN 0-387-98406-2. MR1619036 (See chapter 5.6)
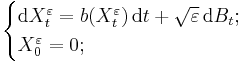
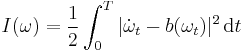
![\limsup_{\varepsilon \downarrow 0} \varepsilon \log \mathbf{P} \big[ X^{\varepsilon} \in F \big] \leq - \inf_{\omega \in F} I(\omega)](/2012-wikipedia_en_all_nopic_01_2012/I/730e7276cca47c17e5d996ebcf6f2148.png)
![\liminf_{\varepsilon \downarrow 0} \varepsilon \log \mathbf{P} \big[ X^{\varepsilon} \in G \big] \geq - \inf_{\omega \in G} I(\omega).](/2012-wikipedia_en_all_nopic_01_2012/I/3e56512f54af5f01493c56fe55b38504.png)